La Elipse

La Elipse.

La elipse es una curva plana, simple y cerrada.

La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante.

Una elipse es la curva cerrada con dos ejes de simetría que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría con ángulo mayor que el de la generatriz respecto del eje de revolución. 

Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado. La elipse es también la imagen afín de una circunferencia.

 

Elementos de una elipse:

 

La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí:

• El semieje mayor (el segmento C-a de la figura), y
• El semieje menor (el segmento C-b de la figura).

Miden la mitad del eje mayor y menor respectivamente.

 

Puntos de una elipse:

Los focos de la elipse son dos puntos equidistantes del centro, F1 y F2 en el eje mayor. La suma de las distancias desde cualquier punto P de la elipse a los dos focos es constante, e igual a la longitud del diámetro mayor (d(P,F1)+d(P,F2)=2a).

Por comodidad denotaremos por PQ la distancia entre dos puntos P y Q.

Si F1 y F2 son dos puntos de un plano, y 2a es una constante mayor que la distancia F1F2, un punto P pertenecerá a la elipse si se cumple la relación:

donde  es la medida del semieje mayor de la elipse.

Ejes de una elipse:

El eje mayor, 2a, es la mayor distancia entre dos puntos opuestos de la elipse. El resultado de la suma de las distancias de cualquier punto a los focos es constante y equivale al eje mayor. El eje menor 2b, es la menor distancia entre dos puntos opuestos de la elipse. Los ejes de la elipse son perpendiculares entre sí.

Excentricidad de una elipse:

 La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (longitud del segmento que parte del centro de la elipse y acaba en uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y uno.

 , con 

Dado que  , también vale la relación:

o el sistema:

La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero. La designación tradicional de la excentricidad es la letra griega ε llamada épsilon.

(No se debe usar la letra e para designarla, porque se reserva para la base de los logaritmos naturales o neperianos. Véase: número e).

Excentricidad angular de una elipse:

La excentricidad angular  es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad , esto es:

Constante de la elipse:

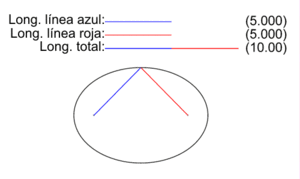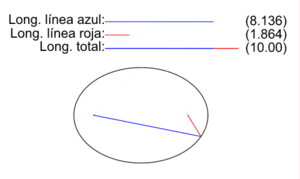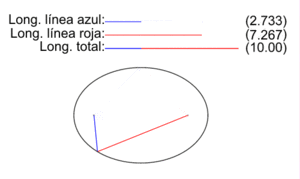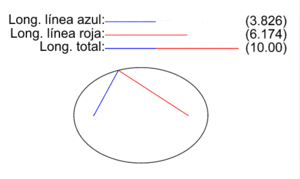 En la figura se muestran los dos radio vectores correspondientes a cada punto P de una elipse, los vectores que van de los focos F1 y F2 a P. Las longitudes de los segmentos correspondientes a cada uno son PF1 (color azul) y PF2 (color rojo), y en la animación se ilustra como varían para diversos puntos P de la elipse.

Como establece la definición inicial de la elipse como lugar geométrico, para todos los puntos P de la elipse la suma de las longitudes de sus dos radio vectores es una cantidad constante igual a la longitud 2a del eje mayor:

PF1 + PF2 = 2a

En la elipse de la imagen 2a vale 10 y se ilustra, para un conjunto selecto de puntos, cómo se cumple la definición.

Elementos gráficos de la elipse:

 Nomenclatura:

La descripción corresponde a las imágenes.

• Los diámetros principales o ejes principales son los diámetros máximo y mínimo de la elipse, perpendiculares entre sí y que pasan por el centro. Tradicionalmente son nombrados A-B el mayor y D-C el menor, aunque también se utilizan otras nomenclaturas, como A-A' el mayor y B-B' el menor.
• El centro de la elipse se suele nombrar O (origen). En la circunferencia los focos coinciden con el centro.
• Los focos se suelen nombrar con la letra F acompañada de algún medio de diferenciarlos, F1 - F2, o F' - F" .
• El diámetro mayor de la elipse se suele designar 2a, siendo a el semieje mayor. El semieje menor se denomina b y eldiámetro menor 2b. La distancia de cada foco al centro se denomina c.
• Los segmentos que van de cada foco a un punto de la elipse se denominan radios vectores; la suma de los radios vectores de cada punto es una constante igual a 2a.

En la imagen vemos algunas otras líneas y puntos importantes de la elipse.

• La circunferencia principal (c. p., en verde) tiene como centro el de la elipse, y como radio a. Se puede definir comoel lugar geométrico de todos los pies de las tangentes a la elipse (como se ve en el ejemplo).
• Las circunferencias focales (c. f., en verde también) son las que tienen como centro cada foco y como radio 2a. Las circunferencias focales y la principal cumplen una homotecia de razón = 2 y centro en cada foco (el de la circunferencia focal contraria).
• La recta t en color cian es una tangente por un punto cualquiera. Al punto de tangencia se lo suele nombrar T, T1, T2, etc. Los segmentos perpendiculares a las tangentes que pasan por los focos, aquí en rojo, se suelen prolongar hasta la circunferencia focal del foco opuesto. No coinciden con la normal a la tangente salvo en los extremos de los ejes principales.
• Los puntos donde se cruzan las normales con sus tangentes son los pies de la tangente. Ese punto pertenece siempre a la circunferencia principal. Al doble de la distancia de F al pie se encuentra el corte de la normal con la circunferencia focal del foco opuesto.