Matrices

Matrices.


En matemát{\displaystyle \mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}\\\end{bmatrix}}}ica, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula(A,B..) y sus elementos con la misma letra en minúscula (a,b...), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.
Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representartransformaciones lineales dada una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.

Operaciones básicas entre matrices.

Las operaciones que se pueden hacer con matrices provienen de sus aplicaciones, sobre todo de las aplicaciones en álgebra lineal. De ese modo las operaciones, o su forma muy particular de ser implementadas, no son únicas.

Suma o adición.

SeanA,B\in {\mathcal {M}}_{{n\times m}}({\mathbb {K}})
{\begin{bmatrix}2&2&1\\3&2&1\\2&3&2\\2&0&4\end{bmatrix}}\quad +\quad {\begin{bmatrix}0&1&4\\1&4&0\\2&1&1\\0&2&2\end{bmatrix}}\quad =\quad {\begin{bmatrix}2&3&5\\4&6&1\\4&4&3\\2&2&6\end{bmatrix}}

Se define la operación de suma o adición de matrices como una operación binaria +:{\mathcal {M}}_{{n\times m}}({\mathbb {K}})\times {\mathcal {M}}_{{n\times m}}({\mathbb {K}})\longrightarrow {\mathcal {M}}_{{n\times m}}({\mathbb {K}}) tal que C=A+B}(A,B)\mapsto C=A+B y donde c_{{ij}}=a_{{ij}}+b_{{ij}}\,\! en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo {\mathbb {K}}. Por ejemplo, la entrada c_{{12}}\,\! es igual a la suma de los elementos a_{{12}}\,\! y b_{{12}}\,\! lo cual esa_{{12}}+b_{{12}}\,\!.
Veamos un ejemplo más explícito. Sea A,B\in {\mathcal {M}}_{{3}}({\mathbb {R}})

{\begin{bmatrix}1&3&2\\1&0&0\\1&2&2\end{bmatrix}}+{\begin{bmatrix}1&0&5\\7&5&0\\2&1&1\end{bmatrix}}={\begin{bmatrix}1+1&3+0&2+5\\1+7&0+5&0+0\\1+2&2+1&2+1\end{bmatrix}}={\begin{bmatrix}2&3&7\\8&5&0\\3&3&3\end{bmatrix}}
No es necesario que las matrices sean cuadradas:
A la luz de estos ejemplos es inmediato ver que dos matrices se pueden sumar solamente si ambas tienen el mismo tamaño. La suma de matrices, en el caso de que las entradas estén en un campo, poseen las propiedades de asociatividad, conmutatividad, existencia de elemento neutro aditivo y existencia de inverso aditivo. Esto es así ya que estas son propiedades de los campos en los que están las entradas de la matriz.
Producto de Matrices.
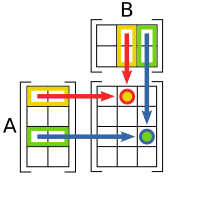
El producto de matrices se define de una manera muy peculiar y hasta caprichosa cuando no se conoce su origen. El origen proviene del papel de las matrices como representaciones de aplicaciones lineales. Así el producto de matrices, como se define, proviene de la composición de aplicaciones lineales. En este contexto, el tamaño de la matriz corresponde con las dimensiones de los espacios vectorialesentre los cuales se establece la aplicación lineal. De ese modo el producto de matrices, representa la composición de aplicaciones lineales.
En efecto, en ciertas bases tenemos que f:V\longrightarrow W se puede representar como f(x)=Ax\,\! donde x\,\! es la representación de un vector de V\,\! en la base que se ha elegido para V\,\! en forma de vector columna. Si tenemos dos aplicaciones lineales f:V\longrightarrow W y g:W\longrightarrow Uentonces f(x)=Bx\,\! y g(x)=Ax\,\!, luego la aplicación g\circ f:V\longrightarrow U se representará como g\circ f(x)=g(f(x))=g(Bx)=ABxdonde AB\,\! es el producto de las representaciones matriciales de f,g\,\!. Nótese que la composición no se puede dar entre cualquier aplicación sino entre aplicaciones que vayan de V\rightarrow W\rightarrow U\,\!, en particular debe de haber una relación entre las dimensiones de los espacios vectoriales. Una vez dicho esto podemos definir el producto de la siguiente manera.
Sean A\in {\mathcal {M}}_{{n\times m}}({\mathbb {K}}) y B\in {\mathcal {M}}_{{m\times p}}({\mathbb {K}}). Se define el producto de matrices como una función {\mathcal {M}}_{{n\times m}}({\mathbb {K}})\times {\mathcal {M}}_{{m\times p}}({\mathbb {K}})\longrightarrow {\mathcal {M}}_{{n\times p}}({\mathbb {K}}) tal que(A,B)\mapsto C=AB y donde c_{{ij}}=\sum _{{k=1}}^{{m}}a_{{ik}}b_{{kj}} para todai,j\,\!, es decir c_{{ij}}=a_{{i1}}b_{{1j}}+a_{{i2}}b_{{2j}}+a_{{i3}}b_{{3j}}+\dots +a_{{im}}b_{{mj}}\,\!. Por ejemplo, la entradac_{{12}}=a_{{11}}b_{{12}}+a_{{12}}b_{{22}}+a_{{13}}b_{{32}}+\dots +a_{{1m}}b_{{m2}}.
Veamos un ejemplo más explícito. Sean A\in {\mathcal {M}}_{{2\times 3}}({\mathbb {R}}) y B\in {\mathcal {M}}_{{3\times 2}}({\mathbb {R}})
{\displaystyle {\begin{bmatrix}\,\,\ \,1&0&2\\-1&3&1\end{bmatrix}}{\begin{bmatrix}3&1\\2&1\\1&0\end{bmatrix}}={\begin{bmatrix}\,\,\,\,1(3)+0(2)+2(1)&\,\,\,\,1(1)+0(1)+2(0)\\-1(3)+3(2)+1(1)&-1(1)+3(1)+1(0)\\\end{bmatrix}}={\begin{bmatrix}5&1\\4&2\\\end{bmatrix}}}
dónde la matriz producto es como habíamos establecido en la definición: una matrizC\in {\mathcal {M}}_{{2\times 2}}({\mathbb {R}}).
Sin tomar en cuenta la motivación que viene desde las aplicaciones lineales, es evidente ver que si ignoramos la definición de la función de producto de matrices y sólo se toma en cuenta la definición de las entradas, el producto no estará bien definido, ya que si {\displaystyle A\,\!}A\,\! no tiene el mismo número de columnas que {\displaystyle B\,\!}B\,\! de filas entonces no podremos establecer en donde acaba la suma: si la acabamos en el mayor de éstos números habrá sumandos que no están definidos ya que una de las matrices no tendrá más entradas, mientras que si tomamos el menor habrá entradas de alguna de las matrices que no se tomen en cuenta. Así es necesario que A\,\! tenga el mismo número de columnas que B\,\! de filas para que AB\,\! exista.
Como se puede suponer también, las propiedades de ésta operación serán más limitadas en la generalidad ya que además de las limitaciones impuestas por la naturaleza de las entradas está esta limitación respecto a tamaño. Es claro, además, que el producto de matrices no siempre es una operación interna.

No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)